0) 개요
generative model 에게 학습한다는 것은 어떤 의미인가???
강아지사진이 여러개 주어졌을 때 우리는 확률분포 p(x) 에 대해 학습하고 싶은 것이다.
1. generation
- 확률분포 p(x) 에서 sample로 만들어낸 x는 강아지처럼 생겨야한다.
2. Desity estimation
- 만약 강아지 사진이 input으로 들어갔을 때 확률분포 p(x)는 높은 값을 가지게 된다.
-> 이렇게 2가지를 할 수 있는 model을 explicit model이라고 한다.
그렇다면 p(x)를 어떻게 나타낼 수 있을까??
0 -1) 기본적인 이산 분포들
1. 베르누이 분포(동전의 튕기기)
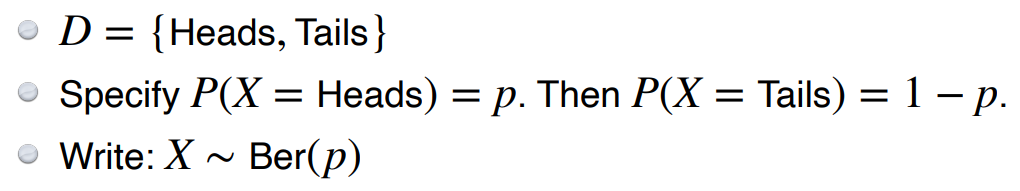
이 분포의 사건은 2가지 결과가 있다. 앞면이 나오거나 뒷면이 나오거나. 따라서 이 분포에서 앞면이 나올 확률만 모수로 지정해주면 뒷면이 나올 확률은 자동으로 알 수 있다.
2. Categorical 분포 (주사위)
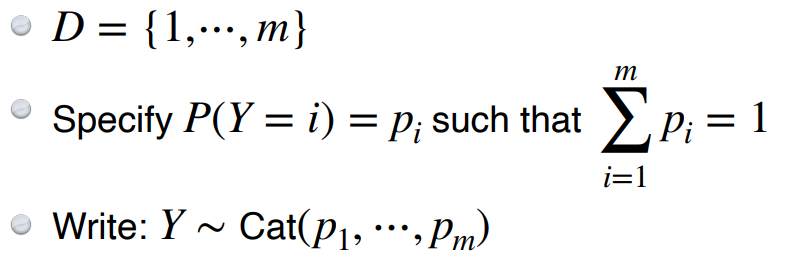
이 분포의 모수는 주사위를 예를 들겠다. 결론은 5개의 모수이다. 왜냐하면 5개의 면의 확률을 명시해주면 마지막면은 자동으로 계산할 수 있기 때문이다.
example
RGB이미지의 1개의 pixel 을 모델링 해보자.

그렇다면 위와 같은 분포를 따를 것이고 이 때 한 픽셀이 가질 수 있는 경우의 수는 256 * 256 * 256이 나올 것이다. 그리고 이 확률 분포의 모수의 갯수는 그것에 1을 빼준 값이 될 것이다.
이렇게 parameter의 갯수를 보면 매우 많다는 것을 알 수 있고 기계학습에서는 파라미터의 숫자가 많은 것은 좋지 않기에 이런 파라미터수를 줄이는 쪽으로 발전하게 되었다.
1) Independence
이제 이미지에서 생각해보자.

n개의 pixel 이 있다고 가정하고 이번에는 rgb가 아니라 흑백 사진인라고 가정한다. 즉 1pixel이 가질 수 있는 경우의 수는 black 아니면 white이다.
그렇다면 전체 이미지의 경우의 수는 2의 n승이 되고 파라미터 수는 그것보다 1 작은 수가 된다.
저런 파라미터의 숫자를가진 확률분포를 모델링하는 것은 불가능하다.

하지만 만약 위의 사건들이 독립이라고 가정한다면 어떻게 될까?? 그렇다면 경우의 수는 같지만 독립사건의 공식에 의해 parameter의 수가 n개가 된다. 독립이기 때문에 모든 항에 대해서 parameter 수를 고려하지 않고 각 pixel 에 대한 parameter로 따로따로 확률분포의 모수로 표현할 수 있기 때문이다.
2의 n승 개에서 n개로 파라미터 수가 줄었다. 이것은 Independence assumption을 했을 때의 결과이다. 이는 파라미터의 수는 줄지만 유의미한 분포를 모델링하기에는 좋지 않다. 즉 표현할 수 있는 표현력을 강제로 줄인 것이다.
따라서 우리는 위 두가지 예제의 중간을 찾고 싶은 것이다. 파라미터의 수가 적절히 줄면서 표현력까지 잘 잡을 수 있는 그 어딘가의 있는 분포를 말이다.
이렇게 해주기 위해 3가지의 규칙이 있다.

먼저 chain rule을 적용해보자
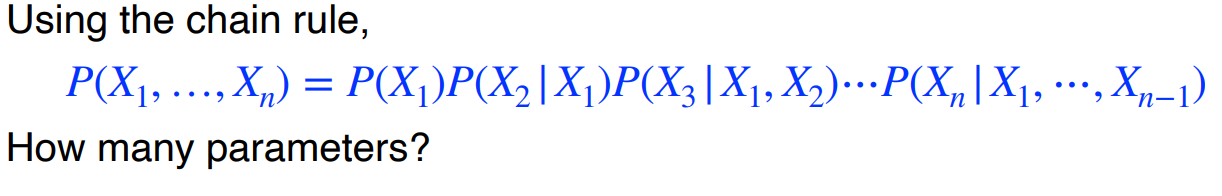
그렇다면 parameter의 갯수가 몇개가 될까??

처음의 결과와 같다. 왜냐하면 원래 joint distrubution을 쪼갠 거와 마찬가지라서 그렇다.
여기서 markov assumption을 다시 한번 가정해보자. markov assumption이란 바로 전 사건만 현재의 사건에 영향을 미친다는 가정이다.

그렇다면 parameter의 갯수는 줄어줄어 2n - 1개가 된다.
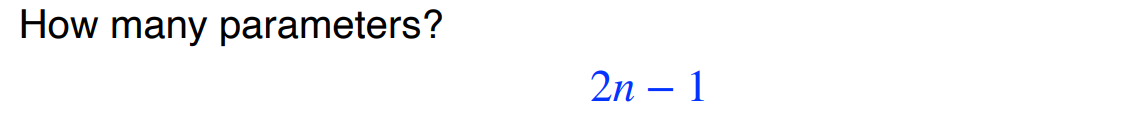
이러한 결과로서 조건부 독립을 적용한 parameter는 전체 독립일 때의 parameter 갯수인 n 과 전체 독립이 아닐때의 parameter의 갯수 2 의 n승에 사이에 있다.
Autoregressive model은 이러한 조건부 독립을 넣어 정의가 가능하다.
2) Autoregressive model
위의 방법을 그대로 적용하면 된다. chain rule 을 사용해서 markov assumption을 활용하여 joint distribution을 쪼갠다. 그리고 지금의 pixel은 전 pixel에만 영향을 받기 때문에 순차적으로 생성하게 된다. 이러한 모델을 autoregressive model이라고 한다. 이렇게 정의된 autoregressive model은 3차원이나 2차원의 이미지를 1차원으로 쭉 펴주는 ordering이라는 것이 필요하다.
Autoregressive Model 특징
1. sampling이 쉽다.
- 이미지를 생성할 때 순차적으로 생성하기 때문이다. 하지만 속도가 느리다. 왜냐하면 이전 pixel이 계산되어야 다음 픽셀도 계산될 수 있기 때문에 병렬처리를 하지는 못한다.
2. exlicit model 이다. < -> implicit model (ex. GAN)
- Autoregressive model은 generate도 되지만 density를 계산할 수도 있다. 이러한 density를 계산하지 못하는 모델도 많기 때문에 이는 장점이라고 할 수 있다. 또 이런 density를 계산할 때는 쪼개서 연산할 수 있기 때문에 병렬처리가 가능하다.
3. 연속확률변수에도 적용할 수 있다.
- Autoregressive model은 연속확률변수에도 적용할 수 있는 확장성이 있다.
NADE(Neural Autoregressive Density Estimator)
이러한 모델의 대표적인 예로 NADE(Neural Autoregressive Density Estimator)라는 것이 있다. density 즉 input으로 넣었을 때 이 이미지가 얼마나 label에 가까운지를 표현하는 정도는 어떻게 계산 될까?
만약 784개의 pixel image가 있다고 가정하면 이 pixel 들은 확률분포의 joint distribution에 대입해 각각의 값들을 알 수 있고 이 값들을 곱한다면 확률분포에 대한 값이 나오게 된다.
'AI > Deep Learning' 카테고리의 다른 글
| CNN (Alexnet, GooLeNet, VGG, ResNet, DenseNet) (0) | 2023.03.26 |
|---|---|
| Generative Model 2(VAE, GAN, Diffusion) (0) | 2023.03.26 |
| Optimizer (0) | 2023.03.24 |
| Transformer (0) | 2023.03.23 |
| RNN(Recurrent Neural Networks) (0) | 2023.03.22 |
0) 개요
generative model 에게 학습한다는 것은 어떤 의미인가???
강아지사진이 여러개 주어졌을 때 우리는 확률분포 p(x) 에 대해 학습하고 싶은 것이다.
1. generation
- 확률분포 p(x) 에서 sample로 만들어낸 x는 강아지처럼 생겨야한다.
2. Desity estimation
- 만약 강아지 사진이 input으로 들어갔을 때 확률분포 p(x)는 높은 값을 가지게 된다.
-> 이렇게 2가지를 할 수 있는 model을 explicit model이라고 한다.
그렇다면 p(x)를 어떻게 나타낼 수 있을까??
0 -1) 기본적인 이산 분포들
1. 베르누이 분포(동전의 튕기기)
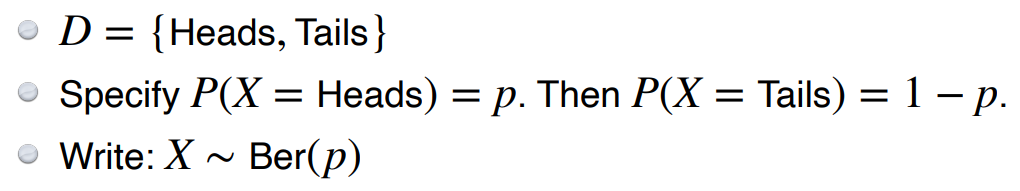
이 분포의 사건은 2가지 결과가 있다. 앞면이 나오거나 뒷면이 나오거나. 따라서 이 분포에서 앞면이 나올 확률만 모수로 지정해주면 뒷면이 나올 확률은 자동으로 알 수 있다.
2. Categorical 분포 (주사위)
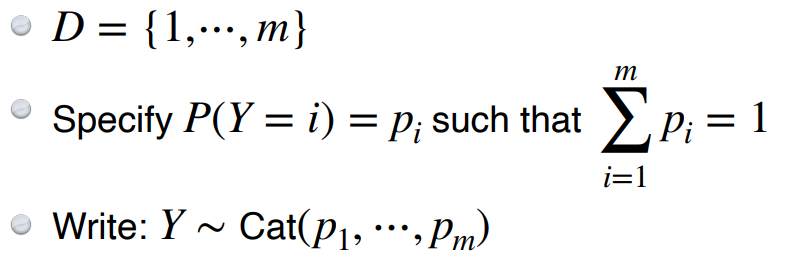
이 분포의 모수는 주사위를 예를 들겠다. 결론은 5개의 모수이다. 왜냐하면 5개의 면의 확률을 명시해주면 마지막면은 자동으로 계산할 수 있기 때문이다.
example
RGB이미지의 1개의 pixel 을 모델링 해보자.

그렇다면 위와 같은 분포를 따를 것이고 이 때 한 픽셀이 가질 수 있는 경우의 수는 256 * 256 * 256이 나올 것이다. 그리고 이 확률 분포의 모수의 갯수는 그것에 1을 빼준 값이 될 것이다.
이렇게 parameter의 갯수를 보면 매우 많다는 것을 알 수 있고 기계학습에서는 파라미터의 숫자가 많은 것은 좋지 않기에 이런 파라미터수를 줄이는 쪽으로 발전하게 되었다.
1) Independence
이제 이미지에서 생각해보자.

n개의 pixel 이 있다고 가정하고 이번에는 rgb가 아니라 흑백 사진인라고 가정한다. 즉 1pixel이 가질 수 있는 경우의 수는 black 아니면 white이다.
그렇다면 전체 이미지의 경우의 수는 2의 n승이 되고 파라미터 수는 그것보다 1 작은 수가 된다.
저런 파라미터의 숫자를가진 확률분포를 모델링하는 것은 불가능하다.

하지만 만약 위의 사건들이 독립이라고 가정한다면 어떻게 될까?? 그렇다면 경우의 수는 같지만 독립사건의 공식에 의해 parameter의 수가 n개가 된다. 독립이기 때문에 모든 항에 대해서 parameter 수를 고려하지 않고 각 pixel 에 대한 parameter로 따로따로 확률분포의 모수로 표현할 수 있기 때문이다.
2의 n승 개에서 n개로 파라미터 수가 줄었다. 이것은 Independence assumption을 했을 때의 결과이다. 이는 파라미터의 수는 줄지만 유의미한 분포를 모델링하기에는 좋지 않다. 즉 표현할 수 있는 표현력을 강제로 줄인 것이다.
따라서 우리는 위 두가지 예제의 중간을 찾고 싶은 것이다. 파라미터의 수가 적절히 줄면서 표현력까지 잘 잡을 수 있는 그 어딘가의 있는 분포를 말이다.
이렇게 해주기 위해 3가지의 규칙이 있다.

먼저 chain rule을 적용해보자
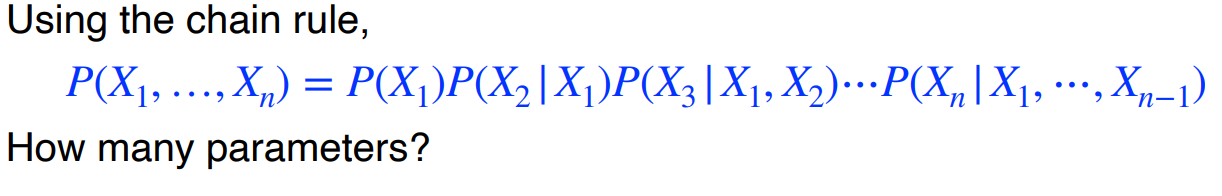
그렇다면 parameter의 갯수가 몇개가 될까??

처음의 결과와 같다. 왜냐하면 원래 joint distrubution을 쪼갠 거와 마찬가지라서 그렇다.
여기서 markov assumption을 다시 한번 가정해보자. markov assumption이란 바로 전 사건만 현재의 사건에 영향을 미친다는 가정이다.

그렇다면 parameter의 갯수는 줄어줄어 2n - 1개가 된다.
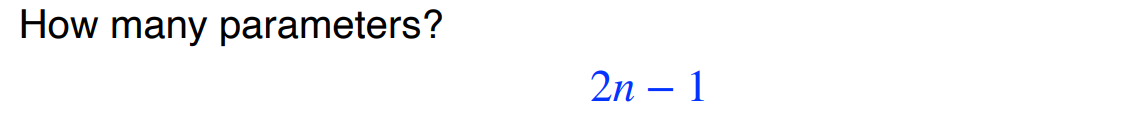
이러한 결과로서 조건부 독립을 적용한 parameter는 전체 독립일 때의 parameter 갯수인 n 과 전체 독립이 아닐때의 parameter의 갯수 2 의 n승에 사이에 있다.
Autoregressive model은 이러한 조건부 독립을 넣어 정의가 가능하다.
2) Autoregressive model
위의 방법을 그대로 적용하면 된다. chain rule 을 사용해서 markov assumption을 활용하여 joint distribution을 쪼갠다. 그리고 지금의 pixel은 전 pixel에만 영향을 받기 때문에 순차적으로 생성하게 된다. 이러한 모델을 autoregressive model이라고 한다. 이렇게 정의된 autoregressive model은 3차원이나 2차원의 이미지를 1차원으로 쭉 펴주는 ordering이라는 것이 필요하다.
Autoregressive Model 특징
1. sampling이 쉽다.
- 이미지를 생성할 때 순차적으로 생성하기 때문이다. 하지만 속도가 느리다. 왜냐하면 이전 pixel이 계산되어야 다음 픽셀도 계산될 수 있기 때문에 병렬처리를 하지는 못한다.
2. exlicit model 이다. < -> implicit model (ex. GAN)
- Autoregressive model은 generate도 되지만 density를 계산할 수도 있다. 이러한 density를 계산하지 못하는 모델도 많기 때문에 이는 장점이라고 할 수 있다. 또 이런 density를 계산할 때는 쪼개서 연산할 수 있기 때문에 병렬처리가 가능하다.
3. 연속확률변수에도 적용할 수 있다.
- Autoregressive model은 연속확률변수에도 적용할 수 있는 확장성이 있다.
NADE(Neural Autoregressive Density Estimator)
이러한 모델의 대표적인 예로 NADE(Neural Autoregressive Density Estimator)라는 것이 있다. density 즉 input으로 넣었을 때 이 이미지가 얼마나 label에 가까운지를 표현하는 정도는 어떻게 계산 될까?
만약 784개의 pixel image가 있다고 가정하면 이 pixel 들은 확률분포의 joint distribution에 대입해 각각의 값들을 알 수 있고 이 값들을 곱한다면 확률분포에 대한 값이 나오게 된다.
'AI > Deep Learning' 카테고리의 다른 글
| CNN (Alexnet, GooLeNet, VGG, ResNet, DenseNet) (0) | 2023.03.26 |
|---|---|
| Generative Model 2(VAE, GAN, Diffusion) (0) | 2023.03.26 |
| Optimizer (0) | 2023.03.24 |
| Transformer (0) | 2023.03.23 |
| RNN(Recurrent Neural Networks) (0) | 2023.03.22 |
