Generative Model 2(VAE, GAN, Diffusion)
0) Maximum Likelihood Learning

원래 배웠던 Maximum likelihood estimation 랑 같은 개념이다. 강아지 이미지들이 주어지고 강아지를 생성하는 확률분포가 존한다고 가정할 때 우리는 그 모델과 거리를 최소화 하는 방향으로 모델을 만들 수 있다. 이 때 모델을 근사할 때 어떤 기준으로 잘됐는지 기준을 정하는게 중요하다.
이 때 사용할 수 있는 기준이 KL-Divergence이다. 이것을 통해 근사적으로 확률분포 사이의 거리를 추정할 수 있다.

위 식을 간략화 시키면 아래처럼 된다.

P_data : 뭔지는 모르지만 data를 생성하는 분포
P_theta: 학습하는 data로 parameterize 되는 분포
간략화 한 식에서 왼쪽항은 무시할 수 있다. KL-divergence를 최소화시키는 방향으로 학습하려면 뒤에있는식을 최대로 끌어올리면 되고 아래식처럼 나오게 된다.

주의할 점: MLL은 generative model을 구현하는데 가능한 하나의 쉬운 방법일 뿐 generative model = MLL은 아니다.

P_data를 모르기 때문에 empirical log-likelihood 로 근사한다. 원래는 모든 가능한 x에 대해 p_data를 다 계산해서 log theta를 최적화 하는 방향으로 해야겠지만 그렇게 할 수 없으니 D개의 dataset을 P_data에서 나왔다고 가정을 했을 때만 보고 P_theta를 학습한다.

그렇게 근사하면 위식을 최대로 올리는 task가 된다.

이러한 방법의 단점은 dataset의 수가 적으면 정확도가 떨어진다는 거이다.
이러한 방법을 Empirical risk minimization(ERM) 이라고 부른다. 이런 ERM은 한정된 data로만 학습하기 때문에 Overfitting이 잘 일어난다. 100개의 이미지 data를 다 외워서 뱉으면 그냥 data를 쓰는것과 같기 때문에 쓸모가 없다.
이러한 Overitting을 막기 위해 모든 분포에서 문제를 푸는 것이 아니라 hypothesis space(모델 공간)을 줄이는 방법을 사용한다. 물론 이러한 방법은 공간 자체를 한정시켜 성능을 한정시키기 때문에 전체 Generative model 의 성능은 낮아질 수 있다. 따라서 MLL자체가 underfitting 문제에 취약하다는 것을 알 수 있다.
모든 가능한 확률분포의 공간을 사용 못해서 그렇다. 일반적으로 최적화는 gradient descent를 사용하고 그렇다면 미분가능한 함수를 사용해야 한다. 만만한게 가우스분포정도로 한정되어 있기 때문이다. GAN이 발표되기 전까지는 이러한 문제점들 때문에 성능이 제대로 나오지 못했다.

그 외에 기준을 잡는 방법은 KL-divergence외에도 위와 같은 방법 들이 있다.
1) Latent Variable Model (VAE)
auto encoder: 입력이 들어왔을 때 encoder를 거쳐서 latent vector를 만들고 decoder 거쳐서 다시 원래 입력으로 복원하는 network이다.
autoencoder 가 generative model인가?? 아니다. 하지만 Variational Autoencoder는 generative model인데 어떤 것이 달라서 그런지 알아보자.
Variational Autoencoder

일단 목적은 앞에와 같다. x라는 입력이 P_theta에서 나왔다고 가정한다면 x들에 대해 P_theta의 값을 최대화시키는 theta를 찾는 MLE를 하는 것이다.
위에서의 문제점은 확률분포를 확정지어 표현력이 좋지않은 분포를 사용해 underfitting문제가 일어나 출력의 값이 좋지 않았다는 것이다. 여기서는 이러한 문제를 해결하기위해 Variational inference라는 technic을 사용한다.
Variational inference는 내가 찾고자하는 분포가 너무 복잡해 모델링 할 수없을 때 그 분포를 찾을 수 있는 간단한 분포로 근사해보자라는 것이다.

Posterior distribution: data가 주어졌을 때 parameter의 확률분포 Posteror distribution이 많으면 계산을 할 수 가없다. 복잡하기 때문이다.
반면 Varaiational distribution 은 계산이 가능하지만 표현력이 떨어진다.
근데 의문점이 든다. 왜냐하면 Posterior distribution은 계산도 복잡하고 표현할 수 없는어떻게 근사할까?? 이것을 쉽게 해주는 것이 Variational inderence이다.

원래 data가 있는 분포가 있고 Porior distribution이 있을 때 VAE는 Encoder와 Decoder를 학습시킨다. 일반적으로 Encoder를 학습하는것이 Variation inference의 variation distribution이다.


다시 돌아가서 우리는 p_theta를 최대화 시키는 x를 찾으면 되고 적절하게 추가하고 섞어가며 아래와 같이 ELBO와 vatiational Gap으로 식은 나뉘게된다. 뒤에 있는 식은 건드리기 쉽지않다. 따라서 ELBO를 최대화 시키는 쪽으로 학습하게 된다.

이제 ELBO를 또 간략화해보자. 그럼 오른쪽과 같은 수식이 유도된다. Reconstructin Term은 encoder와 decoder를 모두 통과한 효과를 가지고 있고 이를 최대화하면 ELBO가 최대화된다. 즉 auto-encoder의 reconstruction loss 최적화이다.
Prior Fitting Term 같은 경우 미리 정해둔 분포(ex 정규분포)를 encoder에 통과한 분포와 비슷하게 만든다.
즉 위에서 왼쪽항은 최대화하고 오른쪽항은 최소화하면 varational autoencoder가 학습이 된다.
단점
- MLL에서 출발은 했지만 근사를 통해 최적화를 해 encoder decoder를 확률분포라고 볼 수 없다.
- Prior Fitting Term도 미분이 가능해야한다. gradient descent를 활용하기 때문이다. KL-divergence는 기분적으로 적분으로 이루어져 있기 때문에 미분하려면 어렵기 때문에 가우시안 분포를 사용해야하는 제약이 있다.
2) Generative Adversarial Networks (GAN)

GAN은 두가지 네트워크로 구성되어있다. Discriminator를 속이려고 하는 Generator와 그런 Generator를 검거하려고 하는 Discriminator이다.
(data인지 만들어낸 이미지인지 구분한다)
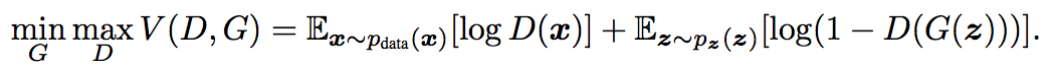
G는 mnimize max는 D는 maximize해야한다. 하지만 이 두개를 동시에 보면서 문제를 보면 어렵기 때문에 한가지를 고정시키고 본다.


Generator 를 고정하고 미분하여 0이되는 optimal discriminator는 위의 식과 같이 나온다.


그리고 위의 optimal discriminator를 식에 적용해 generator의 optimal generator를 구하면 Kenson-Shannon Divergence가 나오고 이는 P_data와 p_G(Generator의 최적화식)의 divergence를 죽이는 것으로 해석할 수 있다.
3) Diffusion Model

diffusion 모델은 노이즈로부터 이미지를 만들어 낸다.
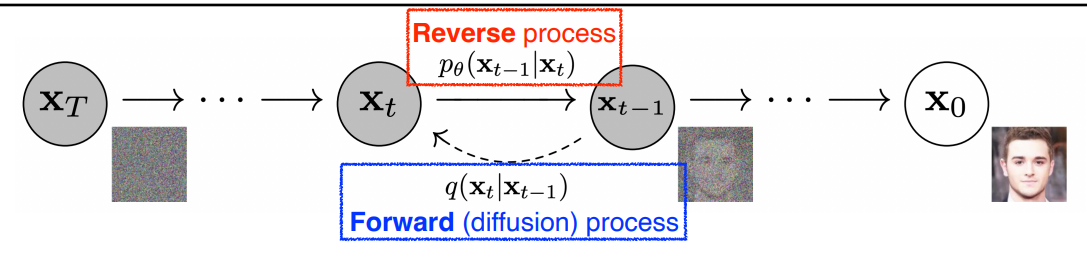
이미지를 만들어낸다기보다 이미지에 노이즈를 집어넣어 노이즈화 시킨다. (Forward process)
학습하는 것은 Reverse process 이다. 노이즈를 없애고 복원하는 것을 학습한다. 서서히 노이즈를 넣으므로 서서히 노이즈를 푼다.
