표본공간(sample space): 시행에서 발생 가능한 모든 경우의 집합
시행(Experiment)
넓은 의미로 받아들여야한다.
시행은 무엇이든 될수있다.
사건(event): 표본공간의 부분집합
확률의 매우 단순한 정의: 사건 A에 대한 확률 P(A) = 표본공간S 경우수 분의 사건A 경우의 수
가정: 모든 경우가 같은 확률로 나온다고 가정한다. 또 가능한 경우(분모)가 유한할때. 항상 이 가정이 만족되는 것은 아니기 때문에 적용 불가능한 경우도 있다.
더보기
단순한 정의를 사용할 수 없을 때
ex) 혜왕성에 생물이 사나??
있거나 없거나 -> 2 분의 1
혜왕성에 지능을 가진 생물이 사나??
있거나 없거나 -> 2분의 1
그러나 직관적으로도 2번째 가정이 확률이 더 낮을 것이라고 생각한다.
이는 확률에 대한 정확한 정의가 없을 때 사람들의 논쟁거리가 되었다.
2가지가 정의 되고 나서 확률이 정립되기 시작.
통계학 -> 직관에 어긋나는 것들 투성이
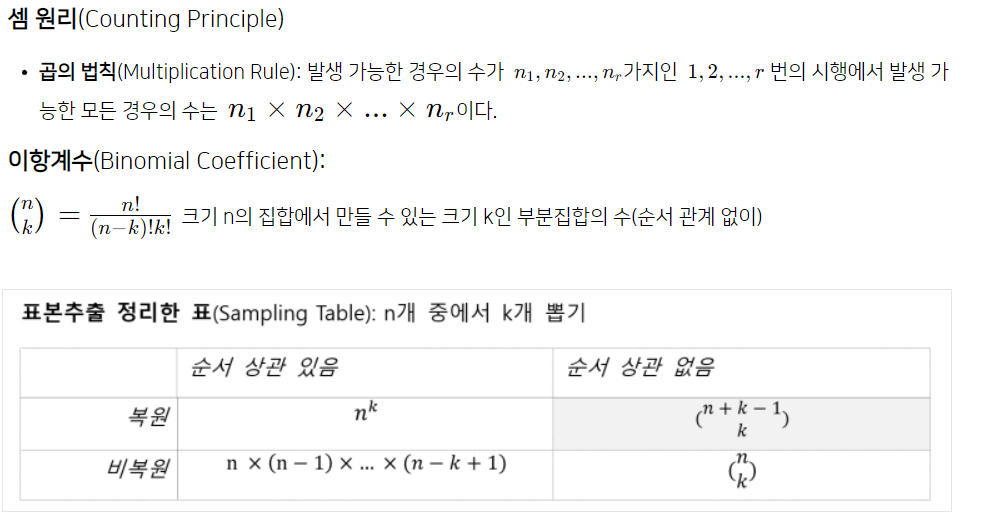
복원 -> 뽑았던 사람이 다시 뽑을 수 있음.
비복원 -> 뽑았던 사람이 다시 뽑을 수 없음.
'수학 > 확률론' 카테고리의 다른 글
| 7강. 확률 변수 (0) | 2023.02.28 |
|---|---|
| 5강. 조건부 확률과 전확률정리 (0) | 2023.02.27 |
| 4강. 조건부 확률 (0) | 2023.02.27 |
| 3강. Birthday Problem과 확률의 특성 (0) | 2023.02.26 |
| 2강. 해석을 통한 문제풀이 및 확률의 공리 (0) | 2023.02.26 |
